The first part of the 6th week of Andrew Ng’s Machine Learning course at Coursera provides advice for applying Machine Learning. In my opinion, this week of the course was the most useful and important one, mainly because the kind of knowledge provided is not easily found on textbooks.
It was discussed how you can diagnose what to do next when you fit a model to the data you have in hand and discover that your model is still making unacceptable errors when you test it under an independent test set. Among the things you can do to improve your results are:
- Get more training examples
- Try smaller sets of features
- Get additional features
- Fit more complex models
However, it is not easy to decide which of the points above will be useful to your particular case without further analysis. The main lesson is, contrary to what many people think, getting more data or fitting more complex models will not always help you to get better results.
Training, cross-validation and test sets
Assume we have a model with parameter vector 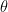 . As I have mentioned here, the training error, which I denote from now on as
. As I have mentioned here, the training error, which I denote from now on as  , is usually smaller than the test error, denoted hereafter as
, is usually smaller than the test error, denoted hereafter as  , partly because we are using the same data to fit and to evaluate the model.
, partly because we are using the same data to fit and to evaluate the model.
In a data-rich environment, the suggestion is to divide your data-set in three mutually exclusive parts, namely training, cross-validation and test set. The training set is used to fit the models; the (cross-) validation set is used to estimate prediction error for model selection, denoted hereafter as  ; and the test set is used for assessment of the generalization error of the final chosen model.
; and the test set is used for assessment of the generalization error of the final chosen model.
There is no unique rule on how much data to use in each part, but reasonable choices vary between  ,
,  ,
,  and
and 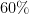 ,
,  ,
,  for the training, cross-validation and test sets, respectively. One important point not mentioned in the Machine Learning course is that you are not always in a data-rich environment, in which case you cannot afford using only
for the training, cross-validation and test sets, respectively. One important point not mentioned in the Machine Learning course is that you are not always in a data-rich environment, in which case you cannot afford using only  or
or 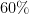 of your data to fit the model. In this case you might need to use cross-validation techniques or measures like AIC, BIC and alike to obtain estimates of the prediction error while retaining most of your data for training purposes.
of your data to fit the model. In this case you might need to use cross-validation techniques or measures like AIC, BIC and alike to obtain estimates of the prediction error while retaining most of your data for training purposes.
Diagnosing bias and variance
Suppose your model is performing less well than what you consider acceptable. That is, assume  or
or  is high. The important step to start figuring out what to do next is to find out whether the problem is caused by high bias or high variance.
is high. The important step to start figuring out what to do next is to find out whether the problem is caused by high bias or high variance.
– Under-fitting vs. over-fitting
In a high bias scenario, which happens when you under-fit your data, the training error  will be high, and the cross-validation error will be close to the training error,
will be high, and the cross-validation error will be close to the training error,  . The intuition here is that since your model doesn’t fit the training data well (under-fitting), it will not perform well for an independent test set either.
. The intuition here is that since your model doesn’t fit the training data well (under-fitting), it will not perform well for an independent test set either.
In a high variance scenario, which happens when you over-fit your data, the training error will be low and the cross validation error will be much higher than the training error,  . The intuition behind this is that since you are overfitting your training data, the training error will be obviously small. But then your model will generalize poorly for new observations, leading to a much higher cross-validation error.
. The intuition behind this is that since you are overfitting your training data, the training error will be obviously small. But then your model will generalize poorly for new observations, leading to a much higher cross-validation error.
– Helpful plots
Some plots can be very helpful in diagnosing bias/variance problems. For example, a plot that map the degree of complexity of different models in the x-axis to the respective values of  and
and  for each of these models in the y-axis can identify which models are suffering from high bias (usually the simpler ones), and which models are suffering from high variance (usually the more complex ones). Using this plot you can pick the one which minimizes the cross validation error. Besides, you can check the gap between
for each of these models in the y-axis can identify which models are suffering from high bias (usually the simpler ones), and which models are suffering from high variance (usually the more complex ones). Using this plot you can pick the one which minimizes the cross validation error. Besides, you can check the gap between  and
and  for this chosen model to help you decide what to do next (see next section).
for this chosen model to help you decide what to do next (see next section).
Another interesting plot is to fit the chosen model for different choices of training set size, and plot the respective  and
and  values on the y-axis. In a high bias environment,
values on the y-axis. In a high bias environment,  and
and  will gradually converge to the same value. However, in a high variance environment there will still be a gap between
will gradually converge to the same value. However, in a high variance environment there will still be a gap between  and
and  , even when you have used all your training data. Also, if you note that the gap between
, even when you have used all your training data. Also, if you note that the gap between  and
and  is decreasing with increasing number of data points, it is an indication that more data would give you even better results, while the case where the gap between them stop decreasing at some specific data set size shows that collecting more data might not be what you should concentrate your focus on.
is decreasing with increasing number of data points, it is an indication that more data would give you even better results, while the case where the gap between them stop decreasing at some specific data set size shows that collecting more data might not be what you should concentrate your focus on.
Once you have diagnosed if your problem is high bias or high variance, you need to decide what to do next based on this piece of information.
What to do next
Once you have diagnosed whether your problem is high bias or high variance, it is time to decide what you can do to improve your results.
For example, the following can help improve a high bias learning algorithm:
For the case of high variance, we could:
- get more data
- try smaller sets of features
- use simpler models
Conclusion
The main point here is that getting more data, or using more complex models will not always help you to improve your data analysis. A lot of time can be wasted trying to obtain more data while the true source of your problem comes from high bias. And this will not be solved by collecting more data, unless other measures are taken to solve the high bias problem. The same is true when you find yourself trying to find more complex models while the current model is actually suffering from a high variance problem. In this case a simpler model, rather than a more complex one, might be what you look for.
References:
– Andrew Ng’s Machine Learning course at Coursera
Related posts:
– Bias-variance trade-off in model selection
– Model selection and model assessment according to (Hastie and Tibshirani, 2009) – Part [1/3]
– Model selection and model assessment according to (Hastie and Tibshirani, 2009) – Part [2/3]
– Model selection and model assessment according to (Hastie and Tibshirani, 2009) – Part [3/3]
– 4th and 5th week of Coursera’s Machine Learning (neural networks)
) happen only in
of the time while cancer-free cases (
) happen
. Then, a silly model that predicts all the cases with
will have only a
error on this dataset. Obviously, this doesn’t mean that this silly model is useful, since it said to the
cancer patients that they are cancer-free.
, what fraction actually has cancer?
) if the probability of success is higher than a given threshold. If we want to predict cancer only if very confident we could just increase this threshold and get a higher precision and lower recall. If we want to avoid missing too many cases of cancer we could decrease the threshold and get a higher recall and lower precision.